Basics of Neural Networks and Deep Learning - Part 4

Course Overview: Deep Learning Course - Overview

We will learn how neural networks are learning (gradient descent), and how neural networks are rated.

Content of this block

The marked article is the current one.

• Our Brain and the Perceptron
• MNIST, and why good data is so important
• Structure of a Neural Network
• A Neural Network is learning
• Backpropagation

How is a Neural Network learning?

There are a few ways for a NN to learn.

• Supervised Learning
• Unsupervised Learning
• Reinforcement Learning

We will focus on the supervised learning first, as we will use it in our first project, but we'll also need the other ones later.

Supervised Learning

-> The NN gets the data and the corresponding label.

This method is usually used for classification tasks, e.g. spam detection or our first project, where we will let the NN clasify images of numbers.

Classification can be separated into binary and multiclass classification.

Binary classification is for example recognizing images of dogs: it's a dog (-> true) or not (-> false).

Multiclass classification would be assigning one of three or more labels, e.g. for images of animals assigning them one of the labels dog, cat, octopus, etc.

Supervised learning is basically what we've been talking about all the time when talking about training.

Unsupervised Learning

-> The NN gets only the data.

With this method we usually try to detect pattern in data and get a rule for this pattern.
This is used in for example recommendation systems.

Reinforcement Learning

-> The NN gets no data, but everything the NN does in a simulated environment is rated.

Reinforcement learning is used to get a NN to work in a real or simulated environment, for example warehouse robots.

Rating our Neural Network

While training the NN, it needs to somehow know which variables (i.e. thresholds, weigths, etc.) it has to improve, and if it has to improve something. For this we are going to calculate the loss, i.e. how much the calculated result is away from the right solution. We will use an error function, also called cost function (or loss function).

The simplest errorfunction is the following:

loss = <right solution> - <calculated solution>

We usually won't use this, as it is not complicated enough for us ;)

We can change this to a more interesting function when for example squaring the result. This would punish errors more.

In reality, it is the sum of the loss calculated with the errorfunction for every variable.

---

Our goal is minimizing the errorfunction, i.e. get a small error. For a normal function we could do so with the derivation.

With the derivation we can get the extreme points of a function, i.e. the minima and maxima.
(To know whether it's a minimum or a maximum we could just insert the x-values into the function...)

Gradient Descent

With all our weights, biases and thresholds, we have much more variables than in a normal function. To make all this more related to the real learning process of a NN, we'll take two variables for our example errorfunction (i.e. three-dimensional space) instead of only one.
Yes that's not much more, but I'm sure you don't want to try to understand all the examples in the 300000-dimensional space ;)

To find the minimum, we will use the gradient.
The gradient gives us the way/direction of the steepest ascent. That may sound cringe and unintuitive first, because why do we need the direction of the steepest ascend when we want to get down?

Well, we'll just 'walk' in the opposite direction, i.e. we can use the negative gradient.
As the gradient is the way of the quick increase, the negative gradient is usually the way of quickest decrease.

For the gradient we'll need the partial derivation for every variable instead of the derivation of the function.

I will explain this detailed in the backpropagation article (the next one)

What we need to know:

When a funtion has many variables and is derivated to one variable, that's a partial derivation.

The gradient tells us which variables are most important / make the greatest change.

Adjusting the variables with the gradient is called gradient descent.

w' = w - n * gradient
with w/w' being the variable / new variable and n the learning rate, i.e. how big the steps of our NN are when improving the variables.

Problems

There are a few important things regarding the gradient descent.
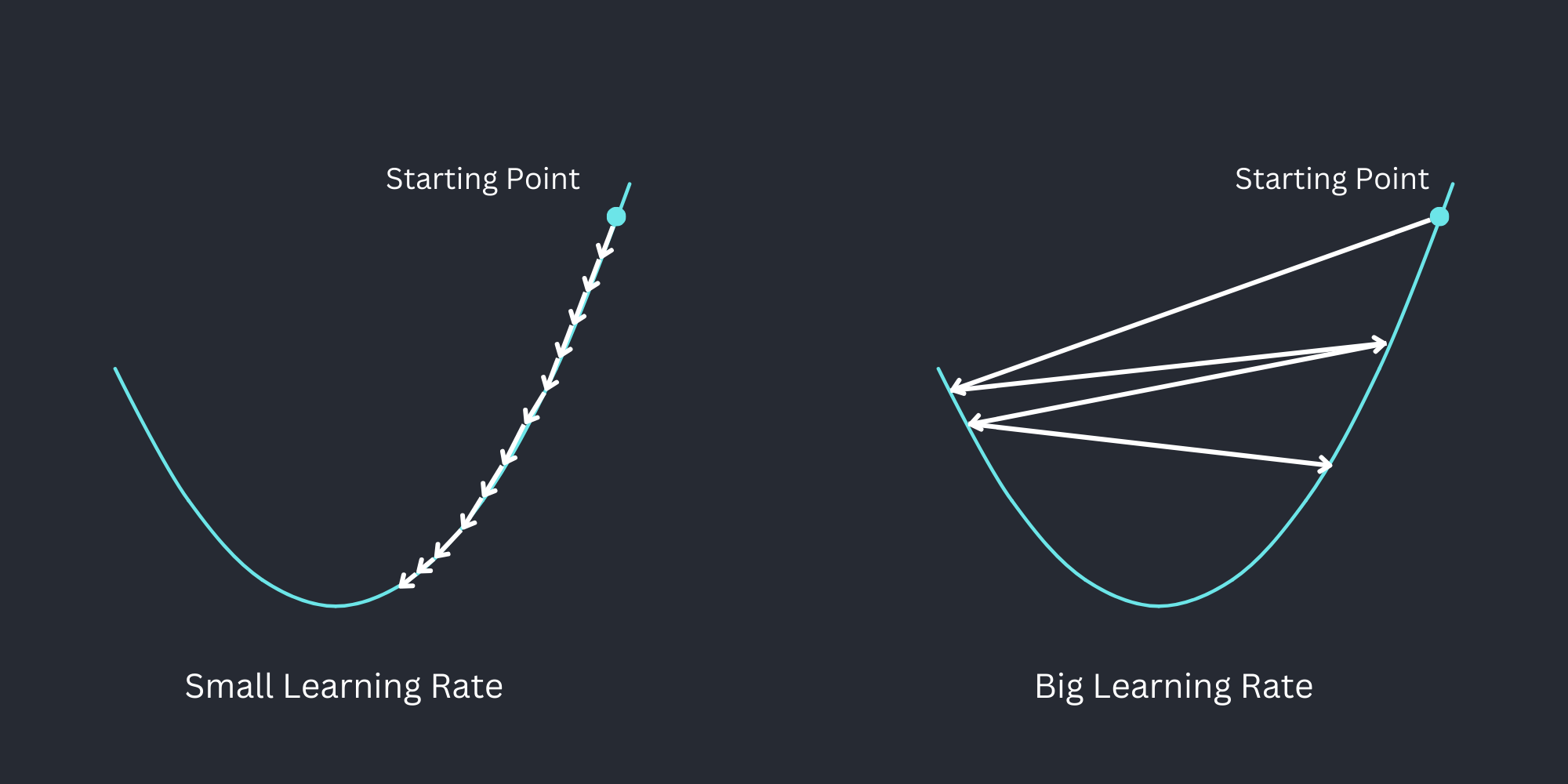
One of them is the right learning rate. If we set it too low, we will have a very long training time because our NN will improve the variables only a little bit every time.
On the other hand we can't set it too high, because this will lead to random behaviour, as we would be jumping from one point to another, maybe without coming closer to the minimum.

Another Problem are local minima. We want to find the minimal point of the whole errorfunction, i.e. the global minimum.

When we take some random starting point, it can happen that the way of quickest decrease, i.e. gradient decent leads us to a local minimum instead of the global one.

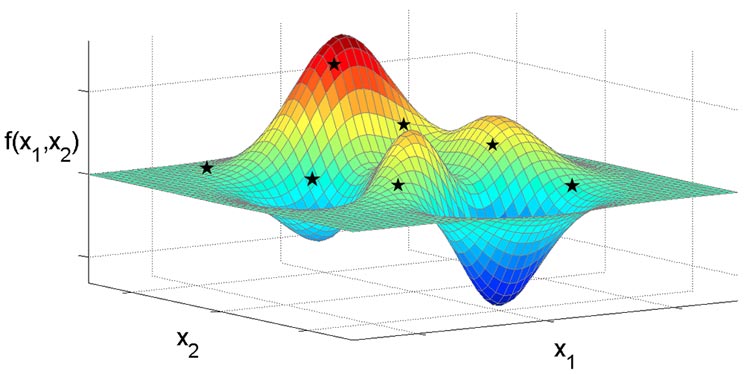
In the picture the left valley is a local minimum, and the right one a global one.

In this case the gradient actually can't help us, because in a local minimum there is no way of decrease near your current point, i.e. the gradient descent always routes us back to the local minimum.

There is no actual solution to this problem, but it's also not an really big problem, because an local minimum is usually quite good to.

If not, just train your NN another time, and the result should be better.

If not, it's probably somehow your fault (or my) :/
But I test all the examples in this course, i.e. they should work.

---

Another point we want to take a look into is the initialisation.

An optimal point for the initialisation would be great, i.e. a point that is already near to a global minimum. Sadly, we don't actually know how to do this either, i.e. we gotta take random values and hope the training helps.

The random values should be in some specific range so we don't have some extreme random values.

Classification of Neural Networks

To classify a NN after training it, and compare it to other neural networks we usually take the accuracy and the loss.

Accuracy is quite self-explainatory:

accuracy = correct classifications / all classifications
i.e. the percentage of correctly classified data.

I've already mentioned the loss, but for a clear definition:
The "loss" measures how far off the network's predictions are from the actual correct answers. The goal during training is to minimize (just like everything ig?) this loss.

For some information while training the NN we can use small parts of the test data to get an accuracy / loss between epochs.

The End

In the next article we will talk about how the NN knows which variables to improve and how much, using the backpropagation algorithm. With this we'll finish the first block.

Next article: work in progress